Planetary Physics

Using observational data obtained by Tycho Brahe, Johannes Kepler (1571 - 1630) determined that 3 laws govern planetary motion. These are: -

  1. The orbit of each planet around the Sun is an ellipse, with the Sun at one focus of the ellipse.
  2. Each planet orbits the Sun in such a way that a line joining a planet to the Sun sweeps out equal areas in equal periods of time, as illustrated below.

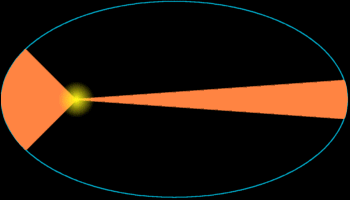
    Illustration of Kepler's second law of planetary motion

  3. The square of the siderial period of each planet is proportional to the cube of its average distance from the Sun ( P2 a a3).

Laws 1 and 2 were first published in Astronomia Nova in 1609, and the third ('harmonic') law was published in Harmonices Mundi in 1619. Kepler's laws were accurate, but based upon observational evidence. The reason why they were accurate was not understood until Newton incorporated his theory of gravity and laws of gravitation, obtaining

P2 = 4p2a3 / G( m1+ m2)

where m1 is the mass of the Sun and m2 is the mass of a planet. Therefore, if P is in years, a is in Astronomical Units (AU), and m is in solar masses,

P2 = a3 / ( m1+ m2)

Retrograde Motion

This phenomenon was first explained by Aristarchus, the ancient Greek astronomer, in terms of a heliocentric universe. (Kaufmann, 1994) He realised that the Earth must be moving in relation to planets further out in order for retrograde motion to be observable.

Retrograde motion animation

Retrograde motion is the apparent east-to-west movement of a planet against the night sky. Usually, planets are seen to move from west to east along the ecliptic (known as direct motion), but sometimes they slow down, stop, and then reverse direction for a period spanning weeks or even months (retrograde motion), before resuming normal direct motion. (Kaufmann, 1994.) The animation above uses the orbits of Earth and Mars to demonstrate the path that Mars follows against background stars.

Later, Ptolemy came up with another idea to explain retrograde motion. It involved a geocentric universe in which all other bodies orbited the Earth on small epicyles circling on their main orbital paths, called deferents. (The illustration below is based on a diagram in Kaufmann, 1994).

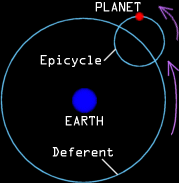
Ptolemy's epicycles and deferents

This was somewhat of a backward step, because the motions of the planets could never be satisfactorily explained in terms of a geocentric universe. The model was tweaked here and there for a long time until it became clear that there was a fundamental problem with it. Copernicus then resurrected the heliocentric model from the ashes, which Galileo proved was correct by observing the phases of Venus in 1610.

The Copernican Model

In 1543, a book by Nicolaus Copernicus (1473 - 1543) called De Revolutionibus Orbium Coelestium (translated as 'On the Revolutions of the Celestial Spheres'), was published. It presented an alternative view of the universe for Man. Until that time, Man was seen as God's greatest creation, and it was believed that God had seen fit to place the Earth at the centre of the universe to symbolise Man's royal position above all other creatures and bodies. Copernicus's book suggested that this was not the case, and that the Sun was at the centre of the universe. He provided compelling mathematical evidence to prove his case, and calculated the distances of the (known) planets from the Sun with surprising accuracy.

However, Copernicus's theory involved perfectly circular orbits for the planets, and therefore could not account for the slight variations in their observed motions, except by using small epicycles for each planet. (Kaufmann, 1994)

Galileo Galilei

From 1610 to 1612, Galileo (1564 - 1642) made several fundamental discoveries with his primitive 2-inch refractor, including :-